Brackett-Serie

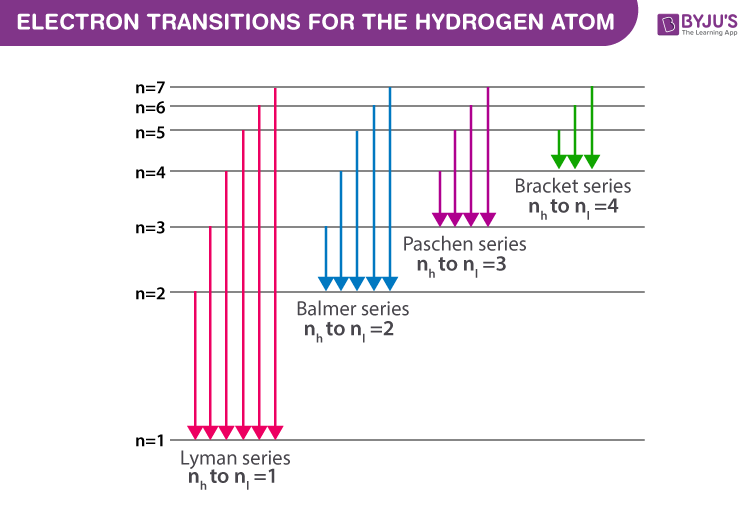
Als Brackett-Serie wird die Folge von Spektrallinien im Spektrum des Wasserstoffatoms bezeichnet, deren unteres Energieniveau in der N-Schale liegt.

Weitere Serien sind die Lyman-, Balmer- (vgl. auch Ausführungen dort), Paschen-, Pfund- und die Humphreys-Serie.

Spektrum

Die Spektrallinien der Brackett-Serie liegen allesamt im infraroten Bereich des Lichts. Sie wurden im Jahr 1922 von dem US-amerikanischen Astronomen Frederick Sumner Brackett entdeckt.

Mathematische Beschreibung

Die Wellenzahlen der Spektrallinien sind durch die Formel

${\displaystyle {\tilde {\nu }}=R_{\infty }\left({1 \over 4^{2}}-{1 \over n^{2}}\right)}$

gegeben. Darin sind

${\displaystyle R_{\infty }=1{,}097\,373\,157\cdot 10^{7}\,{\mathrm {m^{-1}} }}$

die Rydberg-Konstante und ${\displaystyle n}$ ganze Zahlen größer 4.

Die Wellenzahl lässt sich durch die Beziehung

${\displaystyle \lambda ={\frac {1}{\tilde {\nu }}}}$

in die Wellenlänge, bzw. durch

${\displaystyle E={\tilde {\nu }}\cdot c\cdot h}$

in die Energie des zugehörigen Photons umrechnen. In letzterer Formel sind ${\displaystyle c}$ die Lichtgeschwindigkeit und ${\displaystyle h}$ die Planck-Konstante.

Siehe auch

• Moseleysches Gesetz

Einzelnachweise